LLAMO A NUESTRO mundo Planilandia, no porque nosotros le llamemos así, sino para que os resulte más clara su naturaleza a vosotros, mis queridos lectores, que tenéis el privilegio de vivir en el espacio. Imaginad una vasta hoja de papel en la que líneas rectas, triángulos, cuadrados, pentágonos, hexágonos y otras figuras, en vez de permanecer fijas en sus lugares, se moviesen libremente, en o sobre la superficie, pero sin la capacidad de elevarse por encima ni de hundirse por debajo de ella, de una forma muy parecida a las sombras (aunque unas sombras duras y de bordes luminosos) y tendríais entonces una noción bastante correcta de mi patria y de mis compatriotas. Hace unos años, ay, debería haber dicho «mi universo», pero ahora mi mente se ha abierto a una visión más elevada de las cosas.
En un país de estas características, comprenderéis inmediatamente que es imposible que pudiese haber nada de lo que vosotros llamáis género «sólido»; pero me atrevo a decir que supondréis que nosotros podríamos al menos distinguir con la vista los triángulos, los cuadrados y otras figuras, moviéndose de un lado a otro tal como las he descrito yo. Por el contrario, no podríamos ver nada de ese género, al menos no hasta el punto de distinguir una figura de otra. Nada era visible, ni podía ser visible, para nosotros, salvo líneas rectas; demostraré enseguida la inevitabilidad de esto.
Poned una moneda en el centro de una de vuestras mesas de Espacio; e inclinándoos sobre ella, miradla. Parecerá un círculo. Pero ahora, retroceded hasta el borde de la mesa, id bajando la vista gradualmente (situándoos poco a poco en la condición de los habitantes de Planilandia) y veréis que la moneda se va haciendo oval a la vista; y, por último, cuando hayáis situado la vista exactamente en el borde de la mesa (hasta convertiros realmente, como si dijésemos, en un planilandés) la moneda habrá dejado por completo de parecer ovalada y se habrá convertido, desde vuestro punto de vista, en una línea recta.
Lo mismo pasaría si obraseis de modo similar con un triángulo, o un cuadrado, o cualquier otra figura recortada en cartón. En cuanto la miraseis con los ojos puestos en el borde de la mesa, veríais que dejaría de pareceros una figura y que adoptaría la apariencia de una línea recta. Coged, por ejemplo, un triángulo equilátero, que representa entre nosotros un comerciante de la clase respetable. La fig. 1 representa al comerciante tal como le veríais cuando os inclinaseis sobre él y le miraseis desde arriba; las figs. 2 y 3 representan al comerciante como le veríais al acercaros al nivel de la mesa y ya casi en él; y si vuestros ojos estuviesen al nivel de la mesa (y así es como le vemos nosotros en Planilandia) no veríais nada más que una línea recta.
Cuando yo estaba en Espaciolandia oí decir que vuestros marineros tienen experiencias muy parecidas cuando atraviesan vuestros mares y avistan una isla o una costa lejana en el horizonte. Ese litoral distante puede tener bahías, promontorios, ángulos hacia dentro y hacia fuera en cantidades y dimensiones diversas; pero a distancia no veis nada de eso (salvo que se dé el caso de que vuestro sol brille intensamente sobre ellos revelando las proyecciones y retrocesos por medio de luces y sombras), sólo una línea gris ininterrumpida sobre el agua.
Bien, pues eso es justamente lo que nosotros vemos cuando uno de nuestros conocidos triangulares o de otro tipo viene hacia nosotros en Planilandia. Como en nuestro caso no hay sol, ni ninguna luz de ese género que pueda hacer sombras, no tenemos ninguna de esas ayudas que tenéis vosotros en Espaciolandia. Si nuestro amigo se acerca más a nosotros vemos que su línea se hace mayor; si se aleja se hace más pequeña; pero de todos modos parece una línea recta; sea un triángulo, un cuadrado, un pentágono, un hexágono, un círculo, lo que queráis... parece una línea recta y nada más.
Es posible que os preguntéis cómo con estas circunstancias desventajosas somos capaces de distinguir unos de otros a nuestros amigos: pero la respuesta a esta pregunta, muy natural, se dará con mayor facilidad y exactitud cuando pasemos a describir a los habitantes de Planilandia. Permitidme aplazar la cuestión de momento y decir un par de cosas sobre el clima y las viviendas de nuestro país.
, 
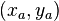, y 
, y los respectivos lados opuestos tienen longitudes 
, 
, y 
, el incentro tendrá por coordenadas: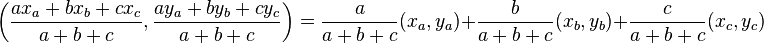
.
